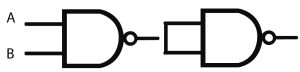NOR & NAND Ou l’universalité du NON-ET

25 Juil 2014 par chris

Le mathématicien George Boole publie en 1854 « An investigation into the laws of Thought » où il donne une forme mathématique aux connecteurs (OU, ET) de propositions vraies (OUI) ou fausses (NON), pour mécaniser la pensée.

Il utilise le principe de contradiction qui stipule qu’une proposition ne peut être, à la fois, vraie et fausse, en excluant leur intermédiaire. Les propositions sont symbolisées par des lettres majuscules A, B, C… et leur inverse ou négation 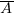, , . La conjonction ET est traduite par le signe x signifiant multiplier. Et la disjonction OU par le signe +.

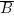
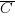
Cette méthode dite « algèbre de Boole » permet de coordonner toute expression. On peut avoir par exemple :

A.C + B + AC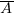

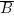
Le coup de génie de Boole fut d’assimiler la façon dont nous pensons et nous exprimons à une symbolique ayant une grande analogie avec l’arithmétique. Raisonner devenait facile. Sans doute cela était trop réducteur mais la physique n’avait-elle pas ramené, avec Newton, le mouvement des corps célestes à une simple formule ? La pensée est également un phénomène physique. N’était-il pas possible de la traiter de la même manière ? Pourtant Hamilton, grand mathématicien s’il en fut, puisqu’il avait condensé la mécanique en deux formules dépouillées, pensait que tout cela était du ressort de la philosophie. Il était en controverse avec De Morgan, à ce sujet, qui soutenait que la logique pouvait être considérée comme une branche des mathématiques. Ce dernier formula une loi qu’on peut résumer ainsi : le contraire d’un composé est l’agrégat des contraires des composants. Ceci peut s’écrire en langage booléen par :

= + ou = .

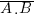
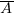
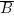
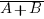
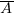
Cela peut se lire NON (A ET B) est équivalent à NON (A) OU NON (B)

Conséquence ahurissante :

La fonction NON-ET (NAND en anglais) est universelle de même que la fonction NON-OU (NOR en anglais). Cela signifie qu’à partir de ces fonctions on peut reconstituer toutes les autres fonctions logiques.

schema1 1/ fonction NON :

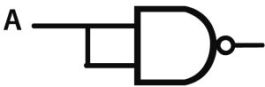
La fonction ET est symbolisée par le petit rond correspondant à sa négation.

L’entrée est A+A qui s’inverse pour donner suivant la loi de De Morgan

= + =

Schema2 2/ De même à partir de deux fonctions NON-ET on peut obtenir la fonction ET

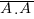
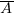
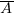
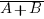
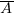
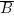
= . + = A.B

3/ Montrons qu’avec NON-ET on peut avoir la fonction OU

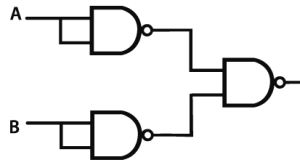
Schema4 La première sortie est + qui devient . = A+B

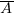
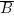
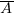
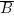
4/Pour être complet

il existe une dernière fonction dite « OU exclusif » symbolisée par A B

Ceci exclue la fonction ET qui est incluse dans A+B. Tout cela est plus compliqué mais parfaitement faisable avec NON-ET

A+B = a+b = (A.B) +(A.B) = (A.B) + (A.B) = A.B.A.B = A.B+AB

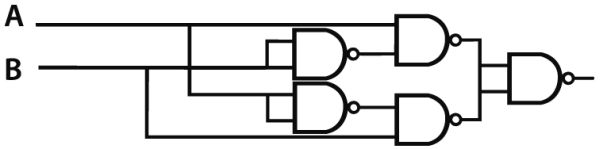
Schema5 5/ On peut aussi à partir de NON-ET monter une bascule.

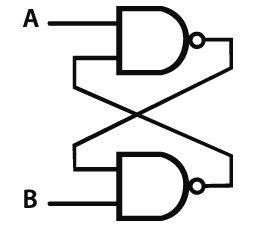
Schema6

Il suffit d’un bref signal sur A ou B pour qu’il y ait une sortie maintenue sur l’une des sorties alors que l’autre sortie n’est pas alimentée. On « bascule » de l’une sur l’autre à volonté avec un seul clic.

Il est fantastique de constater qu’en niant la fonction ET ou la fonction OU on peut construire tout un processus d’enchaînement de propositions.

Les fonctions de base de l’algèbre de Boole peuvent ainsi être reconstituées en les niant simplement. Il peut y avoir là un débat d’ordre philosophique. Il suffit de néantiser le réel pour le reconstituer comme une image dans un miroir le monde se reflète en s’inversant.

C’est parfaitement dualiste. L’univers se divise en « connaissable » et « inconnaissable ».

Le connaissable c’est ce qu’enregistre nos cerveaux et s’accumule dans la mémoire. Or cela ne fonctionne que par « Tout ou rien ». La logique est un langage séquentiel, différentiel et discontinu. On ne perçoit que par sauts. L’uniformité est stérile. La pensée, le langage, les mathématiques, la science permettent seulement de lire dans le grand livre de la nature, comme le disait Galilée. Ce ne sont que des outils pour nous aider à mieux nous retrouver dans un monde confus et difficilement extricable. La carte n’est pas le territoire, le menu n’est pas le repas.

Tout cela n’est qu’une façon de ranger ces notions dans nos tiroirs conceptuels afin de mettre le monde à la portée de nos moyens limités et finis. On ne peut saisir que par opposition. Les couples d’opposés se superposent et s’entassent les uns sur les autres. C’est alors un fatras indémêlable et la seule solution pour notre mental séparateur est de distinguer ce qui nous parait vrai en éliminant le faux résiduel. Il suffit d’enchâsser les uns à la suite des autres ce qui est retenu. La logique est une mise en ordre causale pour éviter de se laisser emporter par le désordre entropique, dans l’ensemble, irréversible.

L’idée extraordinaire de Boole de mathématiser les mécanismes de la pensée et de la communication a permis le formidable essor de la numérisation et de l’informatique en substituant le virtuel au réel. (lire notre article « Pour un oui, pour un non » qui montre que ces deux notions, contraires l’une de l’autre mais indéfectiblement liées, peuvent donner lieu à un nombre fantastique de combinaisons).

La composition des propositions par les connecteurs ET, OU, n’a comme résultat que OUI (tautologie) ou NON (contradiction).

Le dualisme montre ainsi qu’il est bien constitutif de notre monde.

NB : La loi de De Morgan peut se dire de la manière suivante :

Si on inverse la fonction ET ou OU et que l’on inverse le résultat on retrouve la fonction ET ou OU de départ. Il s’agit donc d’une double inversion comme la symétrie miroir ou parité P.

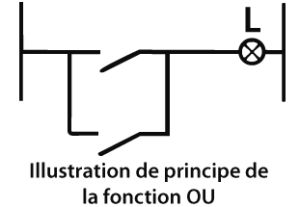
La fonction OU inclusif est parfaitement expliquée par la figure jointe. La lampe L s’allume si on ferme les interrupteurs a ou b et également a et b.

Schema7