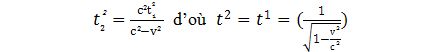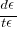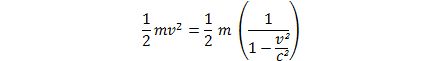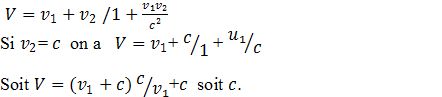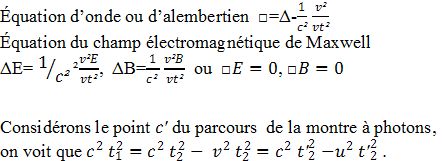Relativité

16 Juil 2015 par chris

 

« Tout est relatif, voilà le seul principe absolu. »

Auguste Comte

Un voyageur doit prendre le train. Il accède au quai le long duquel le train est arrêté. Il y monte et s’installe à la place qui lui a été réservée.

A côté du train il y a un autre train en parallèle, arrêté également. Le voyageur regarde ce train à travers la vitre. Il a soudain la sensation que son train est en train de démarrer. Mais il regarde le quai et s’aperçoit que son train est toujours arrêté. En fait, c’est l’autre train qui vient de démarrer et cela lui a donné l’illusion de son départ. Voilà un premier exemple de relativité. Entre deux mobiles, il n’est pas possible pour un observateur lié à l’un d’eux de déterminer lequel bouge par rapport à l’autre s’il n’y a pas, d’autre part, un repère fixe.

Le train du voyageur démarre, ce qui lui donne l’impression que le quai défile en sens inverse. Le train atteint alors sur une ligne droite, une vitesse régulière de 100 km/h. Le voyageur constate que dans son compartiment, il peut se verser un verre d’eau sans que cette eau ne se répande malgré la vitesse. Tout se déroule comme si le train était à l’arrêt .Une mouche vole tranquillement, indifférente à la vitesse. Il est impossible de savoir si l’on est à l’arrêt ou en mouvement. Un objet sur le porte-bagage tombe. Sa chute apparait verticale comme si le train était à l’arrêt. En fait, par rapport à un observateur situé au sol, la trajectoire est, comme il se doit, une parabole mais comme le train avance au fur et à mesure de la chute de l’objet, les trajectoires coïncident et l’objet est au même endroit que si sa chute était verticale. Pour le voyageur, l’objet est tombé à ses pieds comme si le train était à l’arrêt. En fait, tout ce qui est dans le compartiment possède une impulsion potentielle non manifestée collectivement en fonction de la vitesse du train.

Le voyageur, pour se distraire, regarde le paysage et il le voit tourner autour de lui. Un arbre qui était devant se retrouve derrière. La fixité du sol donne l’illusion d’une rotation du paysage.

Ayant un petit creux, le voyageur décide d’aller manger un sandwich au wagon restaurant. Il empreinte donc le couloir à une vitesse d’environ 2 km/h. Pour l’observateur situé au sol, la vitesse du voyageur est de 100+2 =102 km/h. Il fait nuit et le voyageur allume une lampe torche pour éclairer son chemin. Par un procédé que nous allons éviter de décrire, la vitesse de la lumière qui est de l’ordre de 300 000 km/seconde, est mesurée par le voyageur en marche, le voyageur arrêté et l’observateur situé au sol. Rappelons que cette vitesse est absolument fantastique. Elle met une seconde pour aller de la Terre à la Lune et peut faire l’aller retour Paris-Poitiers, soit plus de 3 600 000 (trois millions six cent mille) fois en une heure. Elle est symbolisée par c (de célérité). Phénomène absolument extraordinaire, on mesure la même valeur dans les trois cas. Pour l’observateur situé au sol, elle devrait être augmentée de 102 km/h. Eh bien non, on trouve toujours la même valeur quelle que soit la direction et la vitesse de l’émetteur. Il faut donc admettre que, pour la lumière, les vitesses ne s’additionnent pas. C’est un fait d’expérience maintes fois répété. Il faut donc se rendre à l’évidence et plutôt essayer de formuler mathématiquement ce constat.

Autre fait qui montre la fragilité du concept de réalité objective ; le voyageur est parfaitement au milieu du train. Avec sa lampe, il lance un signal lumineux vers les deux extrémités du train où un miroir réfléchit le signal. Pour le voyageur, les signaux vont parvenir en même temps à l’avant et à l’arrière du train. L’observateur situé au sol, voit le train arriver sur lui. Il voit donc d’abord le flash de l’avant et ensuite le flash de l’arrière. S’il y a simultanéité pour le voyageur, ce n’est pas le cas pour l’observateur sur le sol. Sa montre lui indiquera un temps plus long que celle du voyageur. Par contre, le train lui paraitra plus court en longueur de la distance parcourue pendant la différence de temps. Les mesures faites au sol ne correspondent pas à celles que pourraient faire le voyageur dans le train.

 

Le train accélère brusquement et le voyageur se trouve enfoncé dans son siège. La mouche se heurte à une vitre. La réalité qui était tranquille jusque là, est bouleversée. Pourtant, si le train avait accéléré très progressivement, nul ne s’en serait aperçu.

Imaginons que le train puisse accélérer jusqu’au voisinage de la vitesse de la lumière. Le temps augmente alors considérablement et l’espace se rétrécit. Par rapport à l’observateur au sol, le voyageur vieillit moins. La grande vitesse le rajeunit en quelque sorte. C’est une bonne cure de jouvence. Par contre, il s’alourdit considérablement. Le train et ce qu’il contient augmente son inertie, sa résistance au mouvement. Plus il accélère, plus il a besoin d’énergie. S’il pouvait parvenir à la vitesse de la lumière, il ne pourrait la dépasser car pour cela il lui faudrait un énorme apport d’énergie. Le voyageur ne vieillirait pratiquement plus.

Que se passe-t-il ?

En fait il y a une vitesse limite sans doute très voisine de celle de la lumière. C’est une constante de la nature appelée c, que l’on ne peut mesurer.

En effet, pour évaluer une vitesse, il faut établir un rapport entre l’espace et le temps mis pour le parcourir. Mais à cette vitesse le temps devient infini et l’espace se réduit à 0. L’inertie devient également infinie. On est face à un mur qu’il est impossible de franchir. Ce n’est pas le mur du son mais le mur de la lumière. La vitesse est indépassable. On sait qu’on utilise le champ électromagnétique ou ondes hertziennes, dont la lumière fait partie, pour transporter de l’information. C’est ainsi que les postes de télévision transmettent images et son. Une conséquence importante de la vitesse. Une limite est que l’on ne peut transférer un message à une vitesse supérieure. On constate que le son d’un reporter est décalé s’il passe par un satellite car la distance à franchir est importante pour l’onde radio.

Revenons à notre voyageur. Il a dans ses bagages un étrange instrument. Il s’agit de deux miroirs parallèles à distance l’un de l’autre. L’objet est posé sur le sol de manière à ce qu’il soit dans le sens de la direction de la vitesse du train.

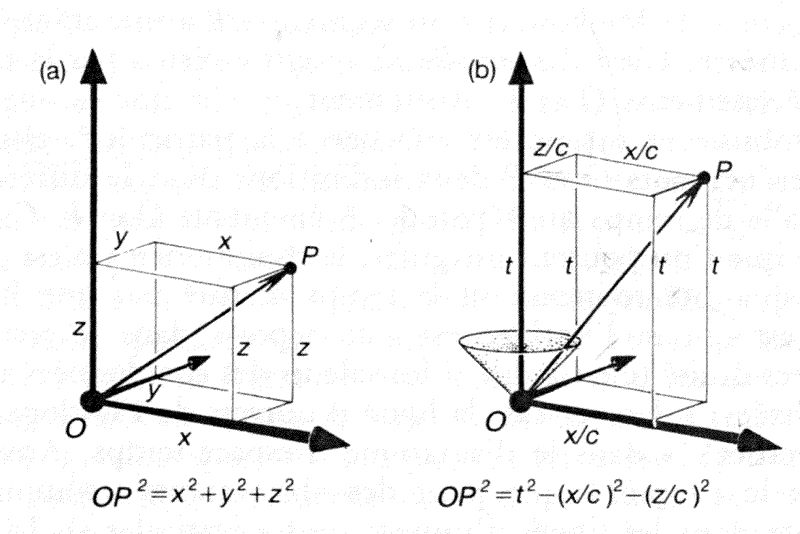
Figure 5.18 La « distance » telle qu’elle est mesurée dans l’un ou l’autre des deux espaces : (a) espace euclidien ; (b) espace de Minkowski où « distance » veut dire « temps vécu »

 

Figure a : il s’agit d’espace euclidien OP² = x²+y²+z²

Figure b : il s’agit d’espace temps de Minkowski. Les coordonnées spatiales sont ramenées à 2 : x et z. Si un rayon lumineux est OP, sa longueur est ct et on a :

c²t²=x² + y² (x² + y² + z² si 3D).

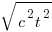
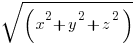
Cela signifie que la distance parcourue par le rayon est identique à la distance euclidienne .

I. Considérations physiques sur la relativité restreinte

 

Qu’il y ait une vitesse limite c peut paraitre bien étrange, mais le physique fonctionne en formulant une théorie qui est vérifiée par de nombreuses expériences. Si les résultats sont cohérents avec la théorie, on la maintient. C’est ainsi que les formulations sur la gravitation de Newton, celles de Galilée sur le mouvement et l’addition des vitesses relatives, celles de Maxwell sur le champ électromagnétique ont été maintenues très longtemps parce que rien ne venait les contredire.

À la fin du 19^ème siècle, une expérience fut réalisée par Michelson et Morley. Le but était de mesurer la vitesse de translation de la Terre sur son orbite, en comparaison avec celle de la lumière. Un interféromètre à deux bras perpendiculaires orienté alternativement dans le sens de rotation était utilisé et les interférences de la lumière venant des deux bras devaient montrer un décalage tel que l’on pouvait calculer la vitesse de translation de la Terre. Or, rien de ce qui était attendu ne s’est produit. L’amélioration de l’appareil disposé aux positions de la Terre en opposition, par exemple en été et en hiver, ne changèrent rien. La vitesse de la lumière n’était influencée ni par la direction du bras, ni par la vitesse de la Terre. La vitesse mesurée de la lumière était toujours la même quelle que soit la position des bras de l’interféromètre et celle de la Terre sur son orbite.

On était obligé de conclure que la relativité Galiléenne ne pouvait s’appliquer quand il s’agissait de la lumière.

On avait aussi constaté que cette relativité ne s’appliquait pas aux formules de Maxwell sur le champ électromagnétique pour un changement de coordonnées d’espace et de temps.

Il fallait donc trouver une autre explication qui est développée dans les considérations mathématiques.

Depuis on a pu, au CERN à Genève, propulser dans un anneau de 27 km de diamètre, des particules comme les protons ou autres, à des vitesses voisines de la vitesse sans jamais l’atteindre. Ces particules développent une durée de vie plus longue et une énorme énergie de collision dont on profite pour les faire éclater. Les formules de la relativité de Lorentz Poincaré s’appliquent parfaitement et sont ainsi vérifiées.

II. Considérations mathématiques

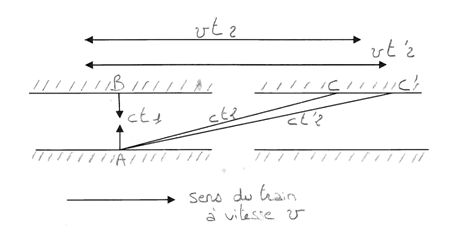
Les deux miroirs parallèles constituent une « montre à photons ». Si cette montre est à l’arrêt, un signal lumineux émis en A  se reflète en B puis à nouveau en A. Si les photons ne sont pas absorbés par les miroirs, ce mouvement de va-et-vient est perpétuel. On appelle cela une symétrie-abyme.

Si le temps mis pour parcourir est  t₁, la distance des deux miroirs s’écrit ct₁ (c étant la vitesse limite).

Le train ayant une vitesse ѵ, la montre se déplace de B en C pendant le temps t₁ de la montre, il met un temps    pour parcourir BC ou BC=ѵt₂.

Pendant le temps  t₂  les photons émis en A se réfléchissent en C. Par conséquent, AC=ct₂.

ABC est un triangle rectangle, on a donc la relation :

 

La valeur de est par conséquent :

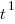
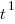
En se déplaçant avec le train, la montre indique un temps t² alors qu’à l’arrêt elle indiquait . En effet pour v=0 les temps et t² deviennent égaux. Par contre si v = c, alors le temps mesuré par la montre devient infini, ce qui n’est pas possible.

La distance parcourue est l’inverse du temps car v=

Si v tend vers c alors les trajets BC et AC ont une tendance à se rencontrer en un point très éloigné qui serait la limite de c. Ce point est à l’infini si les miroirs viennent l’un contre l’autre, ce qui donne à la montre, la mesure d’un temps qui tend vers l’infini.

Il faut donc, au lieu d’additionner les vitesses, utiliser la transformation dite de Lorentz. Quand la vitesse d’un référentiel inertiel (c’est-à-dire en mouvement rectiligne uniforme) augmente, la mesure du temps dans ce référentiel est multiplié par 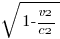que l’on peut symboliser par ɤ. L’espace dans ce référentiel diminue du même coefficient ɤ.

L’énergie du mouvement cinétique est ⅟₂² .

Comme v=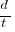  alors v²=

On a d’après les formules précédentes :

L’énergie ou inertie qui est la résistance au mouvement est :

Elle tend vers l’infini si v tend vers c.

Ainsi donc, plus on s’approche de c plus le temps et l’énergie (donc la masse) ont tendance à aller vers l’infini. L’espace, lui, au contraire se rétrécit. Par contre dans tous les référentiels, la limite est c qui est alors une constante universelle. Ceci est très largement confirmé par l’expérience et doit être respecté. Rien ne peut aller plus vite que c.

L’espace et le temps vont varier suivant la vitesse de leur référentiel mais leur rapport ne peut dépasser c.

Cela va conduire Minkowski à l’idée de traiter l’espace comme le temps dans un espace-temps à quatre dimensions.

L’espace perceptible est à trois dimensions. C’est le monde plat euclidien. Dans la figure 5.18, cet espace peut se ramener à la droite OP. Dans la montre à photons on peut considérer la droite  BC comme représentant l’espace réel euclidien qui est celui dans lequel nous vivons. Le temps se déroule indépendamment mais il peut être considéré comme une coordonnée d’espace figuré par la distance BC.

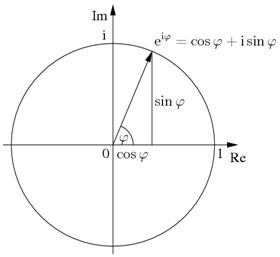
Sa coordonnée espace-temps est AB ou ct qui est perpendiculaire à BC. Comme BC représente les trois coordonnées spatiales, il faut une certaine imagination pour se représenter AB perpendiculaire « à la fois » aux trois axes cartésiens qui sont eux-mêmes perpendiculaires entre eux. Si un axe réel a une base égale à 1, on admet que 1 devient une base imaginaire i par une rotation de 90°, dont le carré i²  est une rotation supplémentaire de 90°ce qui inverse 1 en -1.

Donc  i=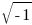 . La coordonnée temps de l’espace temps de Minkowski devient ict et son carré – c²t². Si les trois composantes en espace euclidien sont x, y, z auxquelles on ajoute – c² t² on obtient une quantité  x²+ y²+z² – c² t²=0.

C’est un tour de passe-passe usuel pour les mathématiciens qui permet de réduire les concepts temps et espace à celui d’espace-temps plus maniable.

Rappelons qu’en relativité galiléenne les vitesses de deux mobiles en mouvement l’un par rapport à l’autre s’additionnent : V = v1 + v2.

Pour être compatible avec la relativité restreinte, on adopte la formule :

La vitesse V est égale à c.

Pour mesurer, il faut définir un étalon. Il a été décidé que la valeur de c serait 299.792.458 mètre/seconde (à +/- 1.2).

La seconde est la durée de 9.192.631.770 périodes de la radiation correspondant à la transition entre 2 niveaux superfins de l’état fondamental de l’atome de césium 133. Pour les horloges atomiques utilisant ce procédé on peut avoir un écart entre ces horloges de 0.03 ms (milliseconde) sur un an.

Le mètre est la distance parcourue par la lumière dans le vide pendant une durée égale à 1/299.792.458 seconde soit 1/c dans sa définition légale.

On voit aussi l’intime relation qu’il y a entre le mètre (unité d’espace) et la seconde (unité de temps). Le rapport entre ces deux unités est bien c. Ce sont là des conventions. La vitesse limite ne peut pas être mesurée car dans ce cas, le temps est infini et l’espace nul. Elle est certainement très proche de la vitesse de la lumière dans le vide que, s’il ne contient pas de particules, possède une énergie caractérisée par sa permittivité Ɛo du champ électrique et sa perméabilité µo du champ magnétique. C’est alors défini par 1/c² = Ɛo µo.

On retrouve ce terme dans :

m = E * 1/c2 Formule de Poincaré-Einstein plus connue sous la forme E=mc²

Ceci montre que, quelle que soit la position de la montre à photons, la distance ct1reste invariante. On symbolise ceci par s. Si s est positif, on est du genre temps. Si s=0, la montre à photons se déplace à la vitesse de la lumière c. C’est le genre lumière. Si s est négatif on est dans l’imaginaire et dans le genre espace.

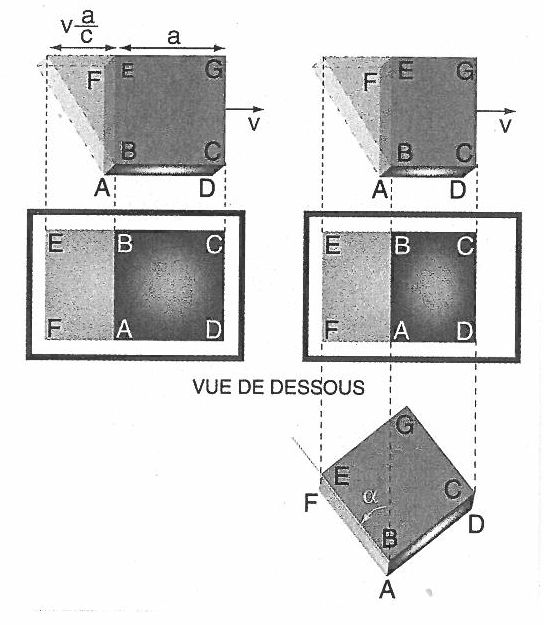
Dans l’espace temps de Minkowski il y a trois coordonnées x, y, z qui mesurent l’espace et une imaginaire qui mesure le temps ct. Ces quatre valeurs constituent un groupe dit de Lorentz-Poincaré dont les rotations représentent les transformations de Lorentz-Poincaré. Pour illustrer ceci, considérons un cube d’arrête a vu du dessus et qui se déplace à la vitesse v. Les rayons lumineux émis par l’arrête EF parviennent à l’observateur à des temps différents. Le décalage est de  a/c par rapport aux rayons émis par AB. Si on prend une photo par-dessus, le cube est déformé. La face ABEF (qui serait invariable si le cube était immobile), apparait avec une largeur v * a/c. Les arêtes du cube orientées dans la direction du mouvement se contractent d’un facteur .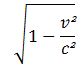

L’arête BC  a une longueur de .

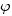
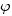
En posant v/c = sin , on constate que tout se passe comme si le cube tournait d’un angle  autour d’un axe parallèle à AB.

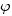
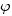
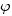
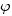
On a vu que v/c=sin comme cos² + sin²c/ =1

est l’angle de rotation du groupe de Poincaré.

La transformation de Lorentz devient 1/cos .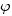

m étant la masse relativiste et m0 la masse au repos, on a :

ce qui donne par un développement en série convergente :

 

Ceci montre que ne peut être atteint que par une progression à l’infini, est l’inertie.

Formule d’Euler

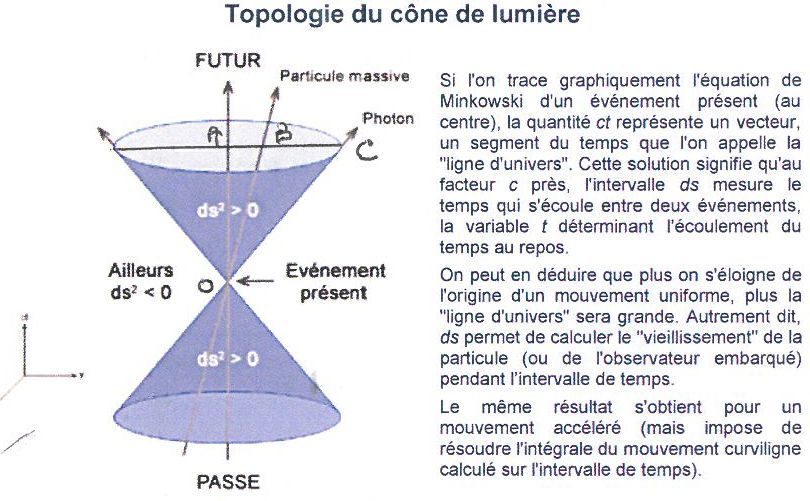
Le cône de lumière illustre l’espace temps de Minkowski. Étant donné l’impossibilité de la figure en quatre dimensions, on n’utilise que deux dimensions spatiales (x, y) et une de temps (ct).

Une particule massive est émise par le présent (0). Le cône est découpé par un plan horizontal qui se déplace en fonction du temps (une coordonnée de temps et pas de coordonnées spatiales).

Si la particule est immobile, elle vit le temps ct(0A). Si elle s’écarte, elle franchit un espace AB. OB est appelé la ligne d’univers . On a 0A²=s² – AB² .

0A est la base de temps liée à la particule. Elle est invariable pour tous points dans le plan AB. Si la particule va en C sa vitesse alors est égale à c car le déplacement spatial AC est égal à OA.

Avec le cône dit, de lumière, on délimite un espace comprenant le passé et le futur. Tout autre événement en dehors du cône ne peut être relié à l’événement 0 car la vitesse qui les joint serait supérieure à c ce qui n’est pas possible. Par la causalité où l’effet suit la cause, l’événement lié à 0 ne peut se produire que dans le cône supérieur. La particule venant de 0 ne peut évoluer que dans le cône futur à condition que sa vitesse soit plus petite que .

III. Considérations philosophiques

Newton distinguait séparément espace et temps en les considérant chacun comme absolus et continus. C’était en fait une sorte de décor ou se déroulaient les événements, sans qu’ils n’influent sur la texture de l’espace qui est homogène et isotrope et du temps qui coule uniformément. Cela signifie qu’une expérience effectuée en n’importe quel lieu et à des instants différents, donne des résultats identiques. Newton avait fait sien le concept de mouvement inertiel de Galilée qui signifie que tout corps ayant une trajectoire rectiligne et une vitesse uniforme ne ressent pas ce mouvement. Tout se passe comme s’il était au repos. Les lois physiques ne sont pas modifiées.

La relativité restreinte ne remet pas en cause la structure de l’espace et du temps et le mouvement inertiel. Par contre, leurs mesures contredisent leur absoluité. Elles sont différentes dans les référentiels Galiléens qui se déplacent les uns par rapport aux autres à diverses vitesses. Les mesures subissent la transformation de Lorentz-Poincaré. Telle qu’elle a été calculée dans les « considérations mathématiques ». Elle est basé de telle façon que la vitesse limite soit indépassable (« considérations physiques »). Dans n’importe quel référentiel un corps ne peut se mouvoir au delà de .

Pour quelle raison est-elle une vitesse limite ? La question serait plutôt comment se fait-il que l’inertie, c’est-à-dire la résistance au mouvement, croit indéfiniment au fur et à mesure que la vitesse s’approche de  c ?

La relativité restreinte se rapporte au champ électromagnétique alors que la relativité générale traite de la gravitation qui se propagerait également à une vitesse limite c.

Le vide pourrait être ce qui reste en l’absence de champ et de particules. Ce vide aurait une perméabilité magnétique symbolisée par « µo » et une permittivité électrique . Un champ électromagnétique pénétrant ce vide rencontre une résistance qui limiterait sa vitesse de telle manière que l’on ait la relation Ɛo µo= 1/c² » qui est le coefficient du carré de la distance spatiale d² pour obtenir le carré de temps t²(d²/c² = t² )

On remarque également que c’est le coefficient de l’énergie du rayonnement électromagnétique E pour obtenir la masse E = mc² -> m=E/c²

m est la masse qui conditionne la gravitation. Ceci pourrait expliquer la vitesse limite des forces électromagnétiques et de gravitation.

Tout n’est que vibration. Comme déjà indiqué, l’espace-temps est défini par les vibrations du césium 133. L’origine résulte d’un coefficient  h ou « constante » de Planck appliqué à l’espace-temps.

En résumé  c est un coefficient appliqué au temps pour obtenir l’espace et à la masse par son carré pour réaliser de l’énergie. h est le coefficient de l’espace-temps pour produire l’énergie-masse.

La vibration introduit une déformation de l’absolu. En découle la notion de relativité qui est justement ce qui n’est pas absolu. On peut donc dire que le monde, tel qu’on le connait, est une conséquence de la relativité et que sans elle, rien n’existerait. Elle brise la continuité. Espace, temps, énergie sont de la pure idéalisation et n’offrent aucune définition péremptoire. Il faudrait pour cela rejeter une vibration à l’identique. Pour cela, il faudrait mesurer cette succession de vibrations et les comparer. Pour ce faire, il faudrait de l’espace, du temps et de l’énergie définis d’une façon absolue. Il est possible de s’approcher au plus prés d’une valeur moyenne inconnue. Plusieurs horloges atomiques finissent certes au bout d’un temps très long à manifester des différences. Si ces horloges dérivent entre elles, c’est qu’elles ne peuvent donner un temps absolu. Toutes les mesures que l’on peut faire, si précises soient elles, n’auront jamais une valeur absolue à laquelle tout pourrait se référer. Seul le relatif est mesurable. Cela génère l’inévitable erreur. Le monde est construit sur la rupture, la brisure, le défaut. L’absolu et la continuité sont inaccessibles. Le contenu exige qu’entre deux points infiniment rapprochés, on puisse toujours en insérer un troisième. Zénon d’Elée avec sa flèche qui, si elle est en mouvement, doit toujours parcourir la moitié du chemin restant. Le mouvement est donc pour lui impossible et n’est qu’une illusion, une apparence. Plus on s’approche d’une hypothétique réalité, plus elle est inatteignable.

L’irréversibilité du temps montre bien que le monde est conditionné par la causalité. L’effet suit apparemment la cause. Nous savons que ceci est du au fait que le désordre prime sur l’ordre, c’est donc une impression générale qui conforte l’idée de l’apparence des événements.

Pour l’espace il n’y a pas de centre qui est partout et nulle part. Quelle que soit la position, le monde se dilate dans toutes les directions. Là aussi l’invraisemblance de ce phénomène enlève à cet espace toute consistance.

L’énergie donne l’illusion d’un mouvement qu’elle provoquerait. Tout ce que l’on peut dire c’est qu’elle se conserve en se transformant. Elle semble inépuisable.

Le temps, l’espace, l’énergie ne sont rien en eux-mêmes. Ils ne sont concevables que par un survol statistique de micro-événements naissant de la probabilité du duo « être / non-être ». Tout vient du néant lieu de calme et de repos, pour s’agiter d’une manière compulsive en s’efforçant désespérément d’y retourner. Mais ils en sont constamment refoulés, le néant voulant conserver son statut.

IV. Relativité générale

La relativité générale concerne la gravitation qui est l’attraction entre les corps massifs. Cette force serait proportionnelle au produit des masses en interaction et comme elle se répand sphériquement elle est aussi inversement proportionnelle à leur distance au carré, la surface développée étant . Cette force est aussi fonction pour un corps de masse de l’accélération de ce corps .

On a donc suivant Newton :

Ceci montre que tous les corps tombent dans le vide avec la même accélération qu’il s’agisse d’une masse de plomb ou de plumes. Ce constat est du à Galilée. Un corps tombe verticalement ce qui, pour lui, est le parcours de moindre effort. En faisant des pirouettes, il dépenserait de l’énergie inutilement.

La relativité générale est mathématiquement compliquée car elle utilise un mode de calcul dit tensoriel et la géométrie sphérique. On peut plus facilement l’expliquer de la façon suivante : on réduit les dimensions spatiales à deux avec un drap. Ce drap est tendu horizontalement par plusieurs personnes. On y pose plusieurs boules massives de tailles différentes. La plus grosse déforme le drap. Si l’on y pose une boule moins massive, celle-ci va être attirée par le creux de la grosse boule. Elle va donc se diriger vers elle et tourner autour. On peut imaginer que l’espace en trois dimensions est comme le drap. Il se déforme suivant la répartition des masses qu’il contient. Il devient courbe au lieu d’être plat comme en relativité restreinte.

De plus les corps ne sont plus en mouvement à vitesse uniforme mais ils sont uniformément accélérés. C’est le cas d’un ascenseur qui tomberait en ayant cassé son câble. Comme dans le mouvement uniforme, tout se passe dans l’ascenseur, comme s’il était au repos. L’uniformité n’est plus dans la vitesse mais dans l’accélération. Une mouche continue à voler comme si de rien n’était.

En relativité restreinte, le mobile parcourt des droites car son espace est plat.

En relativité générale, l’espace est courbe comme par exemple une sphère. Dans ce cas le parcours de moindre action n’est plus une droite mais un arc de grand cercle. Si l’espace à des courbures variées le parcours de moindre action est appelé géodésique.

 

Que se passe-t-il en général ?

Les petites masses sont attirées par les plus grosses mais leur parcours suit ces géodésiques.

Comme l’a bien résumé l’astrophysicien John Wheeler :

La matière dit à l’espace comment se courber.

L’espace dit à la matière comment se mouvoir.

 

Comme en relativité restreinte, la vitesse d’un corps ne peut dépasser celle de la lumière et l’espace et le temps sont confondus en espace-temps qui se courbe suivant la répartition des masses dans l’univers.

Ceci explique que le pendule de Foucault au Panthéon oscille dans un plan constant et révèle ainsi la rotation de la Terre. Son mouvement est en fait dépendant de cette répartition des objets massifs comme les galaxies d’étoiles qui n’évoluent que sur des centaines de milliers d’années. La Terre comme gyroscope, garde un axe de rotation plus ou moins constant pour la même raison.

La relativité générale a été vérifiée par la légère courbe d’un rayon venant d’une étoile pendant une éclipse de soleil et le mouvement du périhélie de Mercure. Elle s’avère utile pour se localiser au mieux possible par le système GPS.

Les trous noirs sont dus à une déformation de l’espace-temps, conséquence de la mort d’une étoile qui s’écrase sous son propre poids. Le nom de trou noir vient du fait qu’il engloutit toute lumière passant dans son environnement.

L’expansion des galaxies n’est en fait qu’une dilatation de l’espace-temps. C’est pourquoi on la décèle quel que soit l’endroit ou l’on se trouve dans l’univers. Autrement dit, il n’y a pas de centre absolu. Il n’y en a que de relatifs les uns aux autres.

En relativité restreinte, la mesure du temps diffère suivant la vitesse relative de chaque référentiel.

En relativité générale, on retrouve les jumeaux dont l’un resté à terre vieillissait plus vite que son frère en déplacement rapide. Dans ce cas, le temps subit une dilatation suivant que l’un est plus accéléré que l’autre. Sur la terre, le jumeau sur une montagne vieillit plus vite que son frère resté en plaine.

Le temps n’est pas absolu, on a l’impression que le temps s’écoule par le fait que l’agitation thermique ou la température diminue en moyenne du fait de l’expansion. Le temps peut ainsi s’assimiler aux vibrations d’une onde électromagnétique par exemple car il y a corrélation entre la température et la fréquence.

Pour des molécules, dans un système isolé l’énergie développée est  constante de Boltzmann et T  = température absolue.

Pour une population de photons également isolée l’énergie s’exprime par E = hf

h est la constante de Planck et f la fréquence.

Temps, température, fréquence ont partie liée avec l’énergie développée. Tout cela n’a que la consistance immatérielle de l’information.

Le probable est le fait d’être plus enclin à être qu’à ne pas être ou l’inverse. C’est donc du relatif qui s’installe entre être et non-être, les deux pôles dualistes du monde.