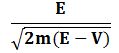La moindre action

13 Oct 2015 par chris

« La nature agit toujours par les voies les plus courtes et les plus simples »

Fermat – 1657

« Etant donné les causes, la nature accouche des effets de la manière qui soit la plus brève possible.»

Léonard de Vinci

« Au commencement était l’action.»

Goethe

« L’action est proportionnelle au produit de la masse par la vitesse et par l’espace .Maintenant voici ce principe si sage, si digne de l’être suprême : lorsqu’il arrive quelque changement dans la nature, la quantité d’action employée pour ce changement est toujours la plus petite qu’il soit possible. »

Pierre Louis Moreau de Maupertuis – 1744

La moindre action

ou l’éloge de la paresse

L’action, on sait intuitivement ce qu’elle évoque d’une façon plutôt imprécise et vague. Ce sont des notions de mouvement, d’activité, de force, d’influence. Newton a postulé que l’action provoque une réaction égale et de sens opposé. On peut dire que l’action fait évoluer un état suivant le temps et l’espace en manifestant de l’énergie. Il s’agit de concepts forgés par l’homme pour mieux appréhender le monde complexe dans lequel il vit. Il prend l’avantage du fait que l’on voit les évènements comme une superposition d’éléments microscopiques, comme une vue d’un avion survolant une mer déchainée. Tout lui apparaît lisse et il en déduit, à tort sans doute, que la nature « obéit » à des lois immuables alors qu’il ne s’agit que d’effet statistique du grand nombre. Tous les concepts qui en résultent comme l’énergie, l’espace, le temps, l’impulsion, la vitesse, la rotation sont indéfinissables en eux-mêmes et n’ont pas de véritable consistance. Mais grâce à notre organe cérébral, on a la faculté d’abstraire ce qui est gênant et de ne conserver qu’une sorte de « grosso modo » suffisamment pratique pour qu’on en déduise un comportement général. On utilise pour cela les mathématiques qui permettent, à partir de postulations, de symboliser les notions qui s’en déduisent d’une façon dite logique. Ceci implique qu’un évènement est la conséquence d’un autre en s’étayant l’un l’autre, d’où il advient une structure qui semble solide. Mais elle peut s’effondrer si le choix oui-non de départ n’est plus possible. On peut réunir les symboles dans des formules qui expriment les liens les réunissant. Ceci permet la concision bien utile pour éviter les raisonnements discursifs.

Il faut scientifiquement définir l’action. C’est ce qui meut dans des degrés de liberté que sont le temps et l’espace, déplacements qui peuvent être linéaires ou rotatifs. Il y a donc une position définie par des coordonnées et la vitesse qui en découle. Pour définir une vitesse suivant l’espace et le temps, il faut deux positions au minimum et admettre de les rapprocher indéfiniment. Les notions de position, de vitesse et de temps peuvent s’exprimer par ce qu’on appelle « lagrangien ». Pour aller d’un point à un autre, il y a une infinité de chemins parmi lesquels il y a une voie où l’action est minimum.

Il nous faut d’abord revenir sur l’affirmation que, quel que soit le changement dans la nature, la quantité d’action nécessitée est toujours la plus petite qu’il soit possible. La nature n’obéit à rien. Elle est fantasque et ses réactions sont souvent imprévues. Tremblements de terre, volcans, inondations et autres catastrophes, du fait qu’elles sont avant tout imprévisibles, sont, bien au contraire, dépensières en action. On peut simplement dire qu’il y a une propension au moindre effort. Cette tendance s’exprime par ce que l’on appelle l’expansion. Cela signifie que l’énergie manifestant un effort d’ordre et de cohérence est disséminée par l’espace-temps. Tout se dégrade par paliers pour aller vers l’étalement où plus rien ne peut se produire.

Le lagrangien est fonction de trois variables : la position spatio-temporelle, la vitesse qui est déterminée en fonction du temps par la variation de la position et le temps.

L’action, en science, est définie comme l’intégrale du lagrangien. C’est la somme de toutes les variations de ce lagrangien relativement aux trois variables liées entre elles. Cette variation doit être nulle entre deux positions qui se rapprochent indéfiniment.

Dans la nature il y a un fonds d’énergie potentiel dans lequel le mouvement puise l’énergie dont il a besoin. Si de l’énergie est empruntée à la nature il faut la lui rendre de telle manière que l’action, produit de l’énergie par le temps, soit conservée, c’est-à-dire que sa variation soit nulle. Si de l’énergie E₁ est prélevée dans un temps t₁, il faut la rendre dans un temps t₂ de telle manière que E₁t₁=E₂t₂. C’est une compensation. Après un tremblement de terre, tout revient petit à petit, dans un temps qui peut être long, à une situation où tout s’efface. Il reste qu’il y a quand même dégradation.

Pour illustrer cela, prenons l’exemple d’une goutte d’eau sur un col qui est comme une selle de cheval. La goutte d’eau en équilibre instable peut le perdre. Elle ira là où il y a déclivité. Entre le col et la vallée il y a une ligne de plus grande pente que la goutte d’eau va s’efforcer de dévaler. Elle peut s’en écarter mais dans ce cas elle monte sur le versant et sera ramenée sur la plus grande pente qu’elle peut traverser. Elle peut ainsi osciller en suivant en moyenne cette plus grande pente qui l’amène par le moyen le plus rapide vers la vallée où elle stagnera jusqu’à repartir vers un endroit plus bas. Ceci est une bonne image du chemin de moindre action. Tout autre itinéraire de la goutte d’eau serait plus dépensier en action.

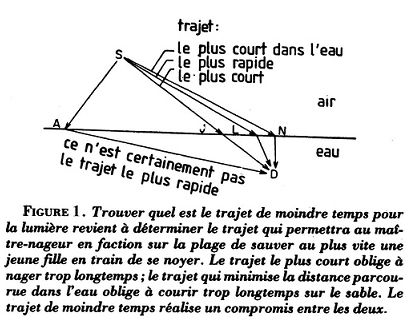
Il y a de nombreux exemples de parcours économiques : la chute verticale des corps pesants, le mouvement rectiligne et uniforme d’un corps sous l’effet d’une impulsion, le trajet de la lumière énoncé par Fermat pour aller d’un point à un autre, la trajectoire d’un obus ou de la terre sur son orbite, les nœuds d’une corde vibrante. Le plus paradoxal c’est ce que doit faire un maître-nageur assis sur la plage pour aller sauver un baigneur en train de se noyer. Sa vitesse étant différente sur le sol et dans l’eau il doit emprunter un parcours moyen.

Il faut noter que dans beaucoup de doctrines et de philosophies on préconise aussi la moindre action. C’est ainsi que selon Aristote on doit chercher à se tenir dans un « juste milieu » et éviter les excès en tout genre.

(voir « le culte du peu » sur le site www.dualisme.com)

Il y a aussi une autre méthode pour rechercher la moindre action que le lagrangien. C’est le « hamiltonien » qui s’avère bien utile en mécanique quantique.

Au lieu de considérer la vitesse, dérivée de la position, on utilise l’impulsion qui consiste à multiplier cette vitesse par la masse du corps qui, elle, est invariable (mv). C’est en quelque sorte une forme d’énergie qui s’exprime selon l’espace alors que l’énergie proprement dite est fonction du temps. Le produit de « mv » par l’espace « d » est aussi de l’action. Le produit mvd est équivalent à E x t, la position étant symbolisée par q.

Le hamiltonien considère la quantité qui est la somme des mv * v = mv². Si le lagrangien est ½ mv²– V (énergie potentielle). En retranchant de mv² on obtient le hamiltonien = ½ mv² + V = + V.

La vitesse v varie de la même façon que et l’accélération c’est-à-dire la dérivée de la vitesse varie de la même façon que l’opposé de par rapport à la position q. Cette relation va faire que q et p sont des variables conjuguées, c’est-à-dire que les produits pq et qp sont différents. Ceci amènera les relations d’indétermination qui feront qu’une précision sur une des données se fait aux dépens de l’autre. Ceci va conditionner toute la mécanique quantique. Position et impulsion sont inconciliables. Elles n’acceptent pas d’être mesurées simultanément. Elles sont inverses comme la transformée de Fourier. Une fonction périodique oscillante s’inverse pour donner la répartition ou le spectre des fréquences correspondantes. Cela est dû à ce que la particule qui ne peut être située exactement en position et vitesse est aussi, à la fois, une onde.

Il y a eu tellement de tergiversations pour déterminer si un être comme le photon ou autres particules sont une particule ou une onde que le physique microscopique a tranché : du point de vue quantique, une particule subatomique est une particule ou une onde, à la fois particule et onde, ni onde, ni particule. Ceci est amplement confirmé.

En ce qui concerne la moindre action, il faut également la considérer de deux points de vue : classique et quantique. La grande différence est que l’option classique considère qu’un corps en mouvement va rechercher le seul chemin possible où l’action est la plus faible. En quantique, on affirme que pour un être microscopique, tous les chemins sont empruntés mais ils sont caractérisés simplement par leur probabilité.

Commençons par la formulation classique.

Le premier à l’énoncer est Fermat en 1655. Il considère la lumière par ses rayons et constate que pour aller d’un point à un autre, elle fera non l’école buissonnière qui lui ferait dépenser beaucoup d’énergie, mais elle prendra le moins de temps possible. Par exemple, réfléchie par un miroir dans le trajet de A à B en passant par le miroir, l’angle d’incidence sera égal à l’angle de réflexion ce qui correspond au moindre temps.

Un siècle après arrive Maupertuis qui introduit le concept d’action comme de l’impulsion (mv) par l’espace parcouru « d ». On dirait maintenant plutôt que l’action est le produit de l’énergie par le temps. C’est donc un effort dans un temps donné. Il affirme que le trajet d’un corps en mouvement s’effectue de telle façon que la dépense en action soit le plus faible possible. Cela donne bizarrement une intention à la nature qui veut dépenser le moins d’action pour aller d’un point à un autre. Mais le constat du parcours d’un corps dans différentes situations le confirme. Dont acte. Il faut évidemment que le corps soit libre de toute influence qui s’opposerait à son déplacement.

C’est ici qu’intervient Lagrange qui veut mathématiser ce phénomène en une formule. Il y a dans l’univers un fonds d’énergie dite potentielle (symbolisée par V). Cela peut être le champ de gravitation où les objets s’attirent proportionnellement à leurs masses et en inverse du carré de leur distance. L’attraction de la terre est la pesanteur. Le corps pour se mouvoir puise dans ce fonds d’énergie. Il dépense alors de l’énergie cinétique (symbolisée par T = ½ mv²). Mais il y a une compensation permanente. Ce qui est prélevé comme énergie E₁ dans un temps t doit être retourné de telle manière que E₁t₁= E₂t₂ peu importe le temps t₂ mis pour rendre l’action. Lagrange considère la quantité d’action T – V dont la variation sera telle que l’intégrale soit minimum. Entre deux positions infiniment rapprochées le corps va dépenser le moins possible d’énergie et en acquérir le plus possible sur le fonds.

Arrive alors Hamilton en 1834 qui donne un tour nouveau aux considérations précédentes. Selon lui, la vitesse est liée à la variation de position q en tenant compte de la masse du corps m. Il conceptualise ainsi la quantité de mouvement mv considérée comme impulsion p et dont la conjonction avec la distance donne l’action. q et p sont alors des grandeurs conjuguées dont le produit n’est pas commutable et qui répondront plus tard aux relations d’indétermination. Le hamiltonien est donc une fonction de q, p et t. L’énergie est égale à E = T+V. Pour obtenir dans ce cas la moindre action cela sera : donc le cumul des variations de T + V. De plus, la grande idée de Hamilton c’est de revenir sur le moindre temps de Fermat qui était valable sous la condition que le milieu parcouru par la lumière soit homogène avec un indice de réfraction n avec la relation de ralentissement n/c si c est la vitesse de la lumière dans le vide. Hamilton considère alors que si n varie régulièrement le corps en mouvement va se comporter de la même manière si le milieu a une valeur continûment variable. Si la lumière est regardée comme une onde, elle se répand en nappes. Si l’indice de réfraction varie progressivement, alors l’onde se déforme, le front d’onde restant perpendiculaire aux axes de propagation. Ce front d’onde a une vitesse que l’on peut calculer de la manière suivante :

L’énergie cinétique T s’écrit ½ mv² d’où l’on peut extraire :

v = avec E – V = T

V est appelé vitesse de groupe. Il y a également une vitesse de phase qui est celle de l’onde lorsque l’indice de réfraction est constant. Cette vitesse peut être c, la vitesse de la lumière dans le vide, qui est une valeur limite.

On peut écrire : c =

devient alors mc et on a c = ou E = mc²

Hamilton aurait pu largement devancer la formule devenu stupidement célèbre E = mc².

On peut également montrer que, compte tenu des acquis futurs, il aurait pu formuler la non moins célèbre équation de Schrödinger dans laquelle le hamiltonien apparaît sous la forme d’un opérateur. On peut ainsi affirmer que Hamilton a été le précurseur de la mécanique quantique. Il a vu plus loin que les autres, ce qui est l’apanage des génies.

Un autre génie est Feynman qui, un siècle environ après, va reprendre l’idée de la moindre action pour la transformer complètement (à noter ce décalage d’un siècle approximativement entre Fermat, Maupertuis, Lagrange, Hamilton et Feynman).Feynman voulait refonder la mécanique quantique en utilisant la notion de moindre action à partir du lagrangien.

Il fut intrigué par un texte de Dirac : pour deux instants voisins t et t+dt, l’amplitude de transition élémentaire est analogue à exp(iS/ħ). Après quelques équations il aboutit à celle de Schrödinger faisant ainsi la démonstration que l’on pouvait établir une mécanique quantique à partir de la formule de l’action de Lagrange qui permettait de retrouver toute la physique newtonienne classique. Le lien entre le classique et le quantique était établi.

Dans son livre « Lumière et matière. Une étrange histoire », il démontre très habilement qu’un corps peut aller d’un point à un autre par tous les chemins possibles y compris les plus farfelus. Ceci allait a contrario de la mécanique classique qui défendait l’idée qu’il n’y a qu’un seul chemin possible, celui qui minimise l’action. A chacun de tous ces chemins éventuels, Feynman associe un nombre complexe exp(iS/ħ) où S est l’action de la particule pour le chemin considéré. Pour lui, c’est une amplitude de probabilité élémentaire correspondant au chemin d’action S. La somme de ces amplitudes élémentaires est l’amplitude de probabilité que la particule se propage d’un point à un autre. Le module au carré de cette amplitude donne la probabilité de propagation de la particule. Le nombre de chemins étant infini, il s’agit de calculer l’intégrale des fonctions de chaque chemin. C’est l’« intégrale de chemin ».

Dans le cas de réflexion par un miroir, est-il possible de retrouver le parcours de moindre temps où l’angle d’incidence est égal à l’angle de réflexion ? On considère que la particule peut se refléter sur n’importe quelle partie du miroir. Dans ce cas les temps de parcours sont plus longs mais la probabilité d’un chemin s’annule par le chemin qui lui est symétrique. Les amplitudes de probabilité des particules sur le chemin de moindre temps, au contraire s’additionnent ce qui confirme le principe de Fermat.

Feynman envisage tous les parcours possibles par réfraction, lentille, etc… La conclusion est toujours la même. C’est le parcours de moindre action qui va réunir les amplitudes de probabilité qui sont plus importantes pour des parcours voisins et deviennent quasi nulles lorsque les trajets sont écartés. Cela rejoint finalement le point de vue classique. La thèse de Feynman transforme les parcours en ceux qui sont les plus probables. La probabilité est reine en mécanique quantique. Mais est-il possible d’envisager que la particule parcourt tous les chemins à la fois ? C’est l’étrangeté du monde quantique. On ne peut dire seulement que les itinéraires sont plus ou moins probables. Une particule en mouvement va naturellement emprunter les voies les plus courtes en fonction de l’occurrence de sa présence.

L’action est l’ingrédient majeur de l’univers dans un sens général. Elle n’est définissable que par le fait qu’elle se conserve dans un système isolé. On ne peut lui donner une consistance. Nous en percevons seulement les effets lorsqu’un évènement s’accomplit. Sa source est intarissable. Son contenant peut être l’espace-temps alors que le contenu est l’énergie. Etant donné qu’elle ne peut être évaluée que par paliers et ne possède aucun point de référence absolue, elle n’a ni centre, ni limites. La seule chose que l’on puisse dire est qu’elle est en expansion que l’on peut sans doute imputer à l’espace-temps. Peut-être y a-t-il un cycle certainement très long d’expansion et ensuite de contraction. Nous vivons dans un univers qui s’étale. Reviendra-t-il à un point de départ avec une énorme concentration d’énergie dans un espace-temps extrêmement réduit ? Et repartira-t-il ensuite vers l’étalement ? C’est probable.

L’action est caractérisée par une alliance de l’énergie et du temps. Si c’est un parcours d’espace, l’énergie est appelée impulsion et se répand sur ses dimensions. Dans ce cas, elle est linéaire mais peut aussi tourner avec un moment cinétique. Cette énergie a pour caractéristique essentielle de pouvoir se transformer sous de multiples aspects. Le contenant a une particularité conventionnelle c’est d’être homogène et isotrope pour l’espace et de s’écouler uniformément pour le temps. Ceci permet qu’un évènement puisse se reproduire à l’identique en tous temps et en tous lieux.

Comment se traduit, dans ce cas de mouvement d’accordéon de l’univers, la moindre action ?

Cette volonté de réduire son effort existe toujours. Mais au fur et à mesure de l’étalement, elle se dilue. Il y a en quelque sorte un jeu de forces dont l’une tend à se concentrer pour se faire disperser par son opposée. Mais dans la période que nous vivons c’est l’étalement donc la dispersion qui l’emporte. C’est la volonté de troubler l’ordre pour semer le désordre. Ce qui se construit est voué à la destruction. Les assemblages de cellules dont nos corps sont composés finissent par se séparer. Nous vieillissons. On va vers la dégradation. L’énergie est écartelée dans son moule d’espace-temps et le produit des deux, soit l’action, l’énergie par le temps, se désintègre.

La volonté de la nature de dépenser le moins possible d’action est favorisée. Cette dépense se fait en puisant dans un inaltérable réservoir. Mais il y a une loi, c’est qu’il doit y avoir compensation. Il faut rendre ce qui est prélevé. Au fur et à mesure que l’univers s’étend, les possibilités de s’approvisionner deviennent de plus en plus rares. On se dirige vers la léthargie. Qu’en sera-t-il si le chemin s’inverse ? Difficile à dire. La mort va-t-elle précéder la naissance ? Ce qui est sûr c’est que nous ne serons plus là pour le constater.

Toute la science physique, absolument toute, s’est construite sur cette tendance de la nature à minimiser ses efforts et cela en constitue la trame la plus simple.

Le grand mathématicien David Hilbert a reconstruit toute la relativité générale d’Einstein à partir de cette idée de moindre action.