La chiralité
« La vie telle qu’elle se manifeste à nous est fonction de l’asymétrie de l’univers et une conséquence de ce fait »
Pasteur
Symétrie
La chiralité
Il n’est absolument pas possible d’enfiler sur la main gauche le gant de la main droite ou l’inverse. C’est de ce constat qu’est né le concept de chiralité (du grec kheir : main). Il s’agit géométriquement de l’image d’un objet dans un miroir. C’est le symétrique par rapport à une ligne ou un plan.
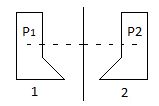
A chaque point P1 de l’objet correspond un point P2 situé de l’autre côté de la ligne et à égale distance. En déplaçant l’objet 1 dans le plan sans le déformer on ne peut jamais le superposer à l’objet 2. La seule chose possible est de retourner l’objet 1 mais dans ce cas, il faut utiliser une dimension d’espace supplémentaire, c’est-à-dire concevoir dans ce cas un espace à trois dimensions. Si l’objet 1 est en trois dimensions il faut utiliser un espace à quatre dimensions qu’on ne peut qu’imaginer. Les objets 1 et 2 sont dits énantiomorphes. Il faut noter que ces objets restent symétriques et conservent la même forme. Il s’agit dans ce cas d’opérations qui ont lieu dans l’espace et le temps comme la translation, la rotation et la conservation. Ce type de symétrie n’est qu’un glissement de ce qui paraît identique dans le même espace-temps. Elle ne présente que peu de contraste. Une symétrie ne peut être qualifiée de telle que si l’on peut faire l’opération inverse c’est-à-dire revenir à la superposition de l’image sur l’objet qui, seule, peut nous garantir qu’il y a bien identité, ressemblance, similitude. Pour avoir des analogies dans les expériences, il faut les réaliser « toutes conditions étant égales par ailleurs ». Pour parler convenablement de symétrie il y a donc lieu d’effectuer le retour inverse pour comparer par identité avec l’objet original.
On peut classer tous les objets qui nous entourent ainsi que les entités, strictement en deux catégories selon qu’ils sont superposables ou non à leur inverse. Un objet appartient nécessairement à l’une de ces classes et ne peut appartenir aux deux à la fois. Si l’objet est superposable à son inverse sans passer par une dimension supplémentaire, il est dit « achiral », comme par exemple une sphère, tout en présentant des axes de symétrie. Un objet « chiral » comme une chaussure, un tire-bouchon, une vis, une coquille d’escargot ne peut coïncider avec son inverse dans le même référent dimensionnel. En résumé si l’on fait subir à un objet quelconque une transformation telle que la rotation, la translation, il n’en est pas affecté s’il est achiral. La chiralité ne modifie pas l’objet mais cet objet et son inverse quoique identiques ne sont pas superposables. On ne peut serrer avec sa main droite que la main droite de l’interlocuteur.
Intéressé par le sujet ?
Voir aussi le livre III La Mêmeté